Metode Transportasi adalah suatu metode yang digunakan untuk mengatur distribusi dari sumber – sumber yang menyediakan produk – produk yang sama di tempat- tempat yang membutuhkan secara optimal. Alokasi produk ini harus diatur sedemikian rupa karena terdapat perbedaan biaya transportasi (alokasi) dari suatu sumber ke beberapa tujuan yang berbeda – beda dan dari beberapa sumber ke suatu tujuan juga berbeda – beda.
Ada tiga macam metode dalam metode transportasi:
- 1. Metode Stepping Stone
- 2. Metode Modi (Modified Distribution)
- 3. MetodeVAM (Vogel’s Approximation Method)
Pada sesi ini hanya akan dibahas mengenai metode transportasi dengan metode stepping stone, metode MODI dan VAM.
Metode Stepping Stone
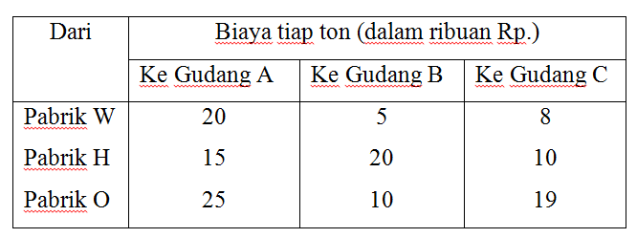
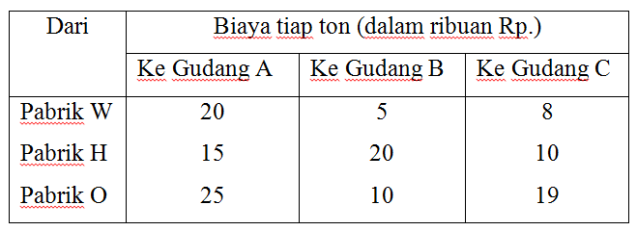
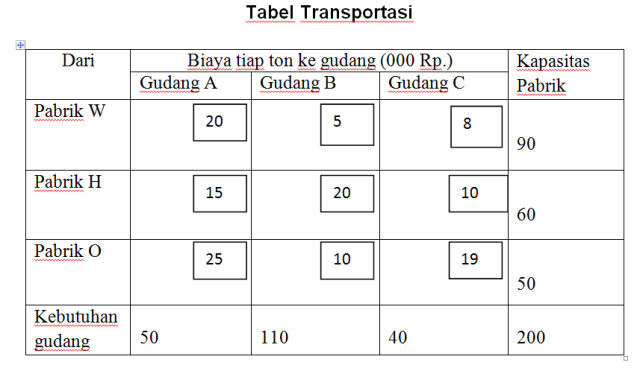
Metode ini dalam merubah alokasi produk untuk mendapatkan alokasi produksi yang optimal menggunakan cara trial and error atau coba – coba. Walaupun merubah alokasi dengan cara coba- coba, namun ada syarat yang harus diperhatikan yaitu dengan melihat pengurangan biaya per unit yang lebih besar dari pada penambahan biaya per unitnya. Untuk mempermudah penjelasan, berikut ini akan diberikan sebuah contoh. Suatu perusahaan mempunyai tiga pabrik di W, H, O. Dengan kapasitas produksi tiap bulan masing- masing 90 ton, 60 ton, dan 50 ton; dan mempunyai tiga gudang penjualan di A, B, C dengan kebutuhan tiap bulan masing- masing 50 ton, 110 ton, dan 40 ton. Biaya pengangkutan setiap ton produk dari pabrik W, H, O ke gudang A, B, C adalah sebagai berikut:
Tentukan alokasi hasil produksi dari pabrik – pabrik tersebut ke gudang – gudang penjualan dengan biaya pengangkutan terendah.
Solusi:
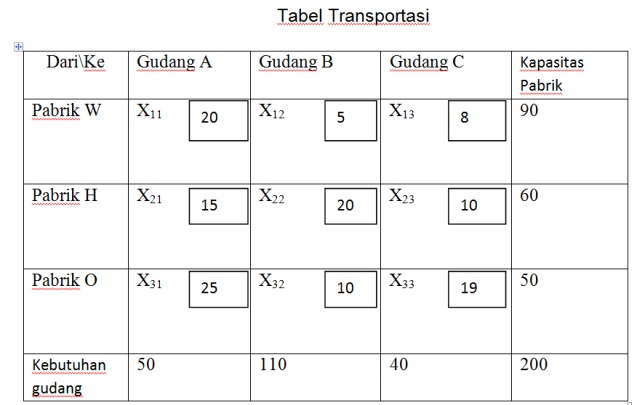
1.1 Penyusunan tabel alokasi
Xij adalah banyaknya alokasi dari sumber (pabrik) i ke tujuan (gudang) j. Nilai Xij inilah yang akan kita cari.
1.2 Prosedur alokasi
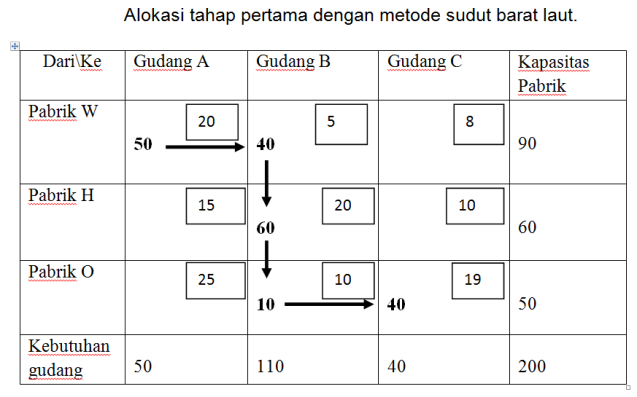
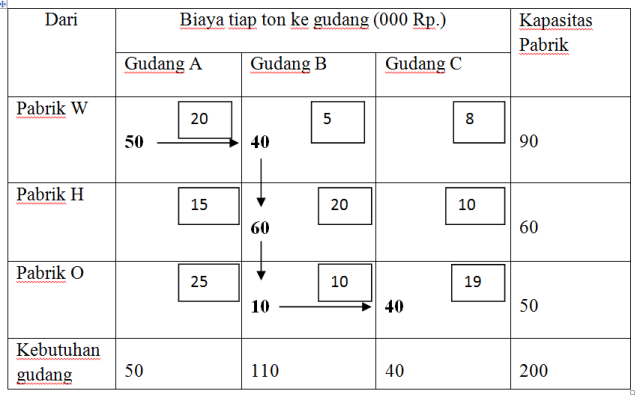
Pedoman prosedur alokasi tahap pertama adalah pedoman sudut barat laut (North West Corner Rule) yaitu pengalokasian sejumlah maksimum produk mulai dari sudut kiri atas (X11) dengan melihat kapasitas pabrik dan kebutuhan gudang.
Biaya Pengangkutan untuk alokasi tahap pertama sebesar =
50 (20) + 40 (5) + 60 (20) + 10 (10) + 40 (19) = 3260.
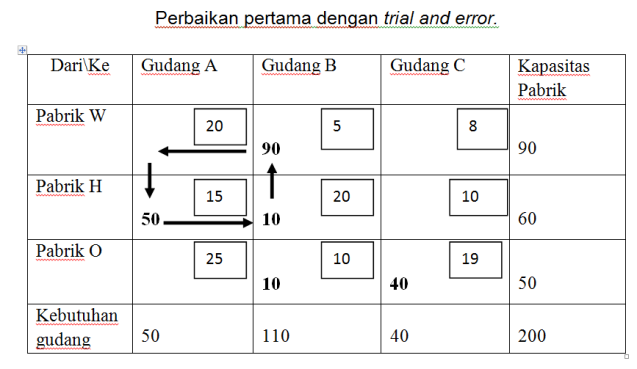
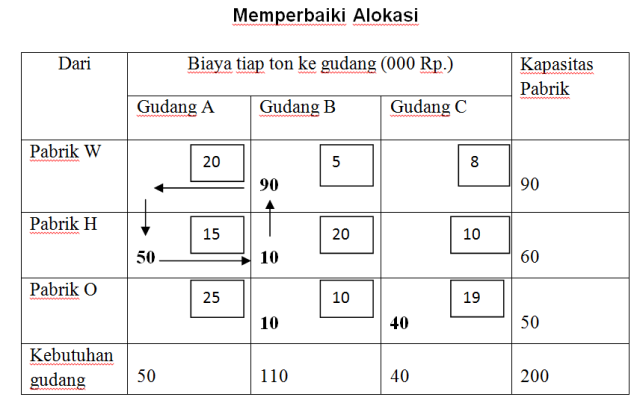
1.3 Merubah alokasi secara trial and error
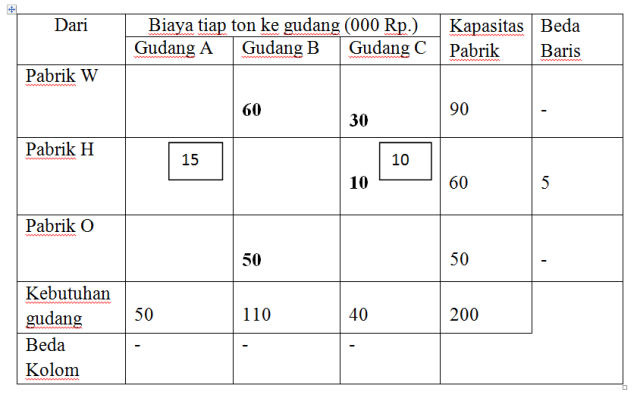
Perubahan bisa dari kotak terdekat atau bisa juga pada kotak yang tidak berdekatan dengan melihat pengurangan biaya per unit yang lebih besar dari pada penambahan biaya per unit. Misalnya akan dicoba perubahan dari kotak WA ke kotak HA artinya 50 ton kebutuhan gudang A akan dikirim dari pabrik H dan buikan dari pabrik W. Perubahan alokasi produk dari dua kotak tersebut akan mengakibatkan berubahnya alokasi produk kotak lainnya yang terkait (kotak HB dan kotak WB). Untuk itu sebelum dilakukan perubahan perlu dilihat penambahan dan pengurangan biaya transportasi per unitnya sebagai berikut:
Penambahan biaya: dari H ke A = 15 Pengurangan biaya : dari W ke A = 20
dari W ke B = 5 + dari H ke B = 20 +
20 40
Karena pengurangan biaya per unit lebih besar dari penambahan biaya maka perubahan dapat dilakukan.
Biaya Pengangkutan untuk alokasi tahap pertama sebesar =
90 (5) + 50 (15) + 10 (20) + 10 (10) + 40 (19) = 2260.
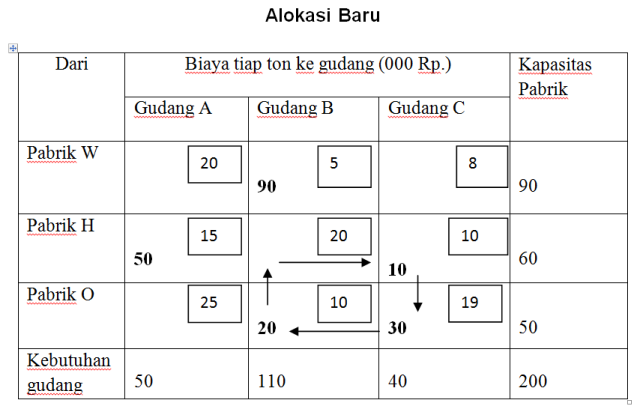
Penambahan biaya: dari W ke C = 8 Pengurangan biaya : dari W ke B = 5
dari O ke B = 10 + dari O ke C = 19+
18 24
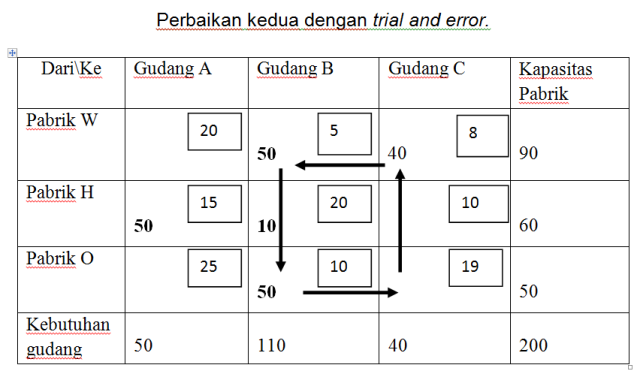
Biaya Pengangkutan untuk perbaikan kedua sebesar =
50 (5) + 40 (80) + 50 (15) + 10 (20) + 50 (10) = 2020.
Penambahan biaya: dari W ke B = 5 Pengurangan biaya : dari H ke B = 20
dari H ke C = 10 + dari W ke C = 8 +
15 28
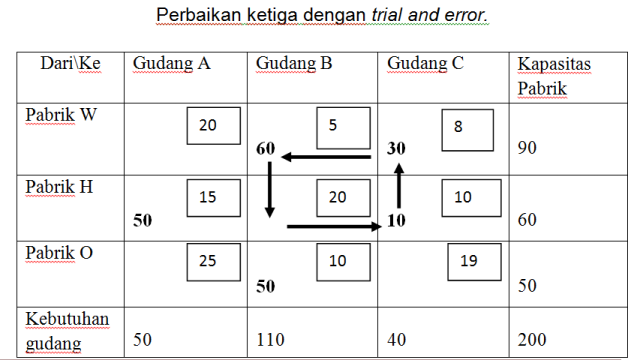
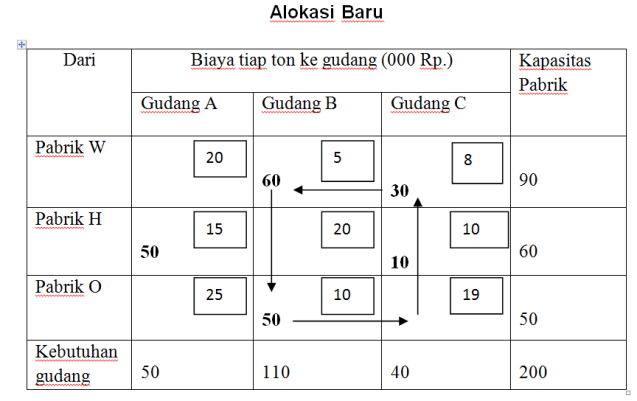
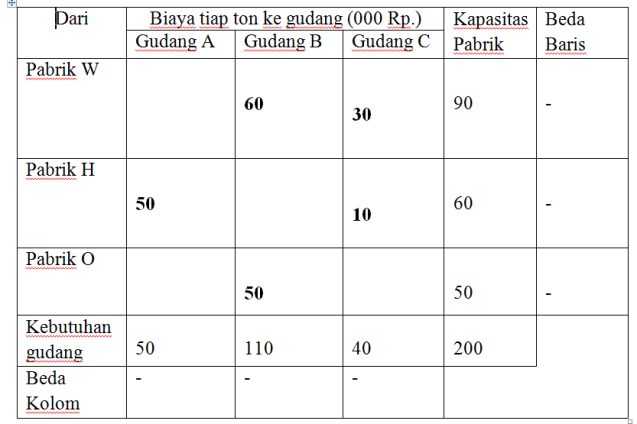
Biaya Pengangkutan untuk perbaikan ketiga sebesar =
60 (5) + 30 (8) + 50 (15) + 10 (10) + 50 (10) = 1890 (biaya pengangkutan terendah)
Sehingga alokasi produksi dengan biaya terendah adalah:
- 90 unit produksi dari pabrik W dialokasikan ke gudang B sebanyak 60 unit dan ke gudang C sebanyak 30 unit.
- 60 unit produksi dari pabrik H dialokasikan ke gudang A sebanyak 50 unit dan ke gudang C sebanyak 10 unit.
- 50 unit produksi dari pabrik O dialokasikan ke gudang B sebanyak 50 unit.
Metode Modi (Modified Distribution)
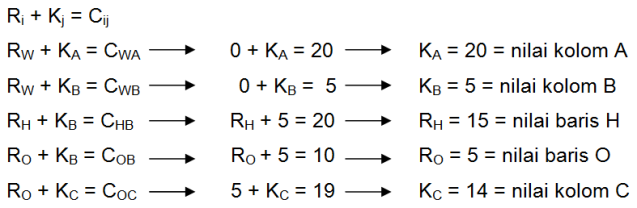
Metode ini dalam merubah alokasi produk untuk mendapatkan alokasi produksi yang optimal menggunakan suatu indeks perbaikan yang berdasarkan pada nilai baris dan nilai kolom. Cara untuk penentuan nilai baris dan nilai kolom menggunakan persamaan:
Pedoman prosedur alokasi tahap pertama mengggunakan prosedur pedoman sudut barat laut (North West Corner rule). Untuk metode MODI ada syarat yang harus dipenuhi, yaitu banyaknya kotak terisi harus sama dengan banyaknya baris ditambah banyaknya kolom dikurang satu. Untuk mempermudah penjelasan, berikut ini akan diberikan sebuah contoh. Suatu perusahaan mempunyai tiga pabrik di W, H, O. Dengan kapasitas produksi tiap bulan masing- masing 90 ton, 60 ton, dan 50 ton; dan mempunyai tiga gudang penjualan di A, B, C dengan kebutuhan tiap bulan masing- masing 50 ton, 110 ton, dan 40 ton. Biaya pengangkutan setiap ton produk dari pabrik W, H, O ke gudang A, B, C adalah sebagai berikut:
Tentukan alokasi hasil produksi dari pabrik – pabrik tersebut ke gudang – gudang penjualan dengan biaya pengangkutan terendah.
Solusi:
1. Isilah tabel pertama dari sudut kiri atas
Biaya pengangkutan untuk alokasi tahap pertama sebesar = 50 (20) + 40 (5) +60 (20) +10 (10) + 40 (19) = 3260.
2. Menentukan nilai baris dan kolom
– Baris pertama selalu diberi nilai nol
Nilai baris W = Rw = 0
– Nilai baris yang lain dan nilai semua kolom ditentukan berdasarkan persamaan
3. Menghitung indeks perbaikan dan memilih titik tolak perbaikan.
Indeks perbaikan adalah nilai dari kotak yang kosong.
Memilih titik tolak perubahan:
– Kotak yang mempunyai indeks perbaikan negatif berarti bila diberi alokasi akan mengurangi jumlah biaya pengangkutan. Bila nilainya positif berarti pengisian akan menyebabkan kenaikan biaya pengangkutan
– Kotak yang merupakan titik tolak perubahan adalah kotak yang indeksnya bertanda negatif dan angkanya besar. Dalam contoh ternyata yang memenuhi syarat adalah kotak HA dengan nilai -20.
Biaya pengangkutan untuk alokasi tahap kedua sebesar = 90 (5) + 50 (15) + 10 (20) +10 (10) + 40 (19) = 2260
4. Ulangi langkah – langkah tersebut diatas, mulai langkah 2.2 sampai diperolehnya biaya terendah, yaitu bila sudah tidak ada lagi indeks yang negatif.
Biaya pengangkutan untuk alokasi tahap ketiga sebesar = 90 (5) + 50 (15) + 10 (10) +20 (10) + 30 (19) = 2070
Biaya pengangkutan untuk alokasi tahap keempat sebesar = 60 (5) + 30 (8) + 50 (15) + 10 (10) + 50 (10) = 1890
Alokasi tahap keempat merupakan alokasi optimal karena indeks perbaikan pada kotak kosong sudah tidak ada yang bernilai negatif.
Metode VAM
Teknik pengerjaan pada metode ini berbeda dengan dua metode sebelumnya yaitu metode transportasi Stepping Stone dan MODI dimana untuk mendapatkan solusi yang optimal dilakukan berulang-ulang sampai kondisi optimal tersebut terpenuhi. Sedangkan pada metoda VAM ini, sekali kita menentukan alokasi pada satu cell maka alokasi tersebut tidak berubah lagi. Untuk mempermudah penjelasan, kita gunakan contoh yang sama seperti pada metode transportasi sebelumnya.
Suatu perusahaan mempunyai pabrik W, H, O dengan kapasitas produksi tiap bulan masing-masing 90 ton, 60 ton, dan 50 ton.; dan mempunyai 3 gudang penjualan di A, B, C dengan kebutuhan tiap bulan masing-masing 50 ton, 110 ton, dan 40 ton. Biaya pengangkutan setiap ton produk dari pabrik W, H, O ke gudang A, B, C adalah sebagai berikut:
Langkah – langkah pengerjaan:
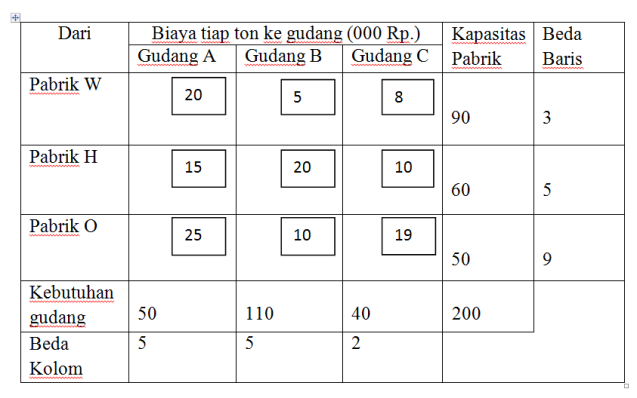
- Susunlah kebutuhan, kapasitas masing-masing sumber dan biaya pengangkutan ke dalam matriks transportasi
2. Carilah perbedaan dari 2 biaya terkecil, yaitu biaya terkecil dan terkecil ke dua untuk setiap baris dan kolom
3. Pilihlah 1 nilai perbedaan- perbedaan yang terbesar diantara semua nilai perbedaaan pada kolom dan baris. Baris O mempunyai nilai perbedaan terbesar yaitu 9. Bila nilai perbedaan biaya ada 2 yang besarnya sama, maka pilihlah baris atau kolom yang mempunyai biaya terendah.
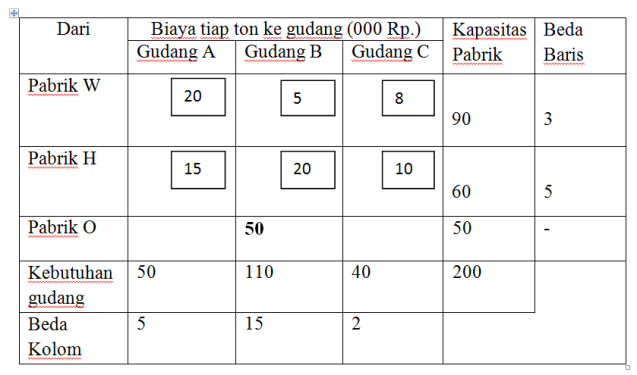
4. Isilah pada salah satu segi empat yang termasuk dalam kolom atau baris terpilih, yaitu pada segi empat yang mempunyai biaya terendah. Isikan sebanyak mungkin yang bisa dilakukan.
5. Karena baris O sudah diisi penuh sesuai dengan kapasitas, maka selanjutnya hilangkan baris O karena baris O sudah tidak mungkin diisi lagi. Kemudian tentukan kembali perbedaan biaya untuk kolom dan baris yang belum terisi. Ulangi langkah-langkah ini sampai semua baris dan kolom sepenuhnya teralokasi.
Karena B mempunyai perbedaan terbesar yaitu 15, maka isilah sebanyak mungkin yang bisa diangkut pada kolom B yang mempunyai biaya terendah.
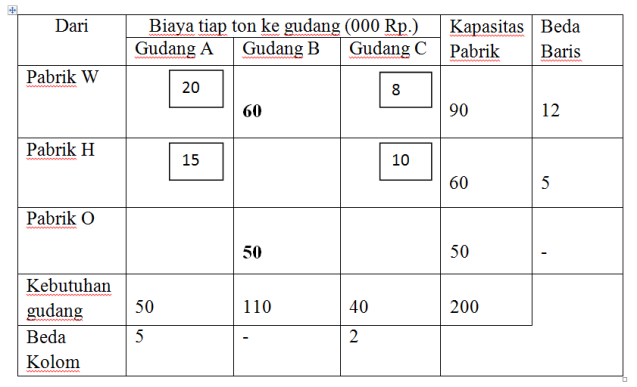
Baris W mempunyai perbedaan terbesar yaitu 12 dan langkah selanjutnya adalah sebagai berikut:
Jadi biaya transportasi yang harus dikeluarkan: 60 (3) +30 (8) + 50 (15) + 10 (10) + 50 (10) = 1890